Aug 19, 04 · f ( x , y ) {\displaystyle f (x,y)} The differential joint entropy h ( X , Y ) {\displaystyle h (X,Y)} is defined as h ( X , Y ) = − ∫ X , Y f ( x , y ) log f ( x , y ) d x d y {\displaystyle h (X,Y)=\int _ { {\mathcal {X}}, {\mathcal {Y}}}f (x,y)\log f (x,y)\,dxdy}The product rule is a formula that is used to determine the derivative of a product of functions There are a few different ways that the product rule can be represented Below is one of them Given the product of two functions, f (x)g (x), the derivative of the product of those two functions can be denoted as (f (x)·g (x))'Where m is the slope The vertex of a quadratic function is calculated by rearranging the equation to its general form, f(x) = a(x – h) 2 k;

Question Video Using The Product Rule Nagwa
F(x+h)-f(x)/h formula name
F(x+h)-f(x)/h formula name-$\dfrac{\Delta y}{\Delta x} = \dfrac{f(ah) – f(a)}{h}$ Now that we know the difference quotient's definition and formula, it's time that we learn how to actually apply them Here are four steps to remember when evaluating difference quotientsFormula f(x) = a(x h) 2 k The Parabola always produces a "U"shaped graph which can open upwards or downwards depending on the value of "a" Given the values of a, h, and k, fill them into the formula to produce the equation of the graph Locating the Axis of Symmetry of a parabola




The Derivative
Calculators and Converters ↳F_m = q v B \sin (\theta) Fm is the magnetic force (due to B) on a charge q moving at a velocity v B the magnetic field θ is the angle between B and the direction of motion of q F_m = I L B \sin (\theta) Fm is the magnetic force (due to B) on a wire with current I and length LWhere x is some point around which we are expanding the Taylor series and h is a small value To recall some terminology, the approximation f(x h) = f(x) is called a zerothorder Taylorseries approximation, while f(x h) = f(x) f (1) (x) h is a firstorder Taylorseries approximationTo view the usefulness of Taylor series, Figures 1, 2, and 3 show the 0th, 1st, and 2ndorder Taylor
Solution We can use the formula for the derivate of function that is the sum of functions f(x) = f 1 (x) f 2 (x), f 1 (x) = 10x, f 2 (x) = 4y for the function f 2 (x) = 4y, y is a constant because the argument of f 2 (x) is x so f' 2 (x) = (4y)' = 0 Therefore, the derivative function of f(x) is f'(xF(x)=\frac{1}{x^2} y=\frac{x}{x^26x8} f(x)=\sqrt{x3} f(x)=\cos(2x5) f(x)=\sin(3x) functionscalculator en Related Symbolab blog posts Functions A function basically relates an input to an output, there's an input, a relationship and an output For every inputFormula Difference quotient = (f (xh)f (x))/h In singlevariable calculus, difference quotient is used to compute the slope for the secant line (ie, the line passes between two points on a curve) between any two points in a graph for the function f
Aug 04, 16 · When working with a function, all you have to do is plug (x h) into your function wherever you see an x Let's look at the function f (x) = 2 x 6 To find our f (x h),Simply substituting x with xh doesn't do it, not to mention that the f's and the coefficients seem to have changed roles, with the f's now being functions instead of constants and the coefficients now being constants instead of functionsH f x −f x −h h f x h −f x −h 2h central difference formula threepoints formula Approximation error Consider the Taylor polynomials and remainder of f x h and f x −h ;




Answered 10 7 Find And Simplify Bartleby




1 For A Function F Use The Fact That F 3 12 Chegg Com
H(x) = f (x)g (x) h ( x) = f ( x) g ( x) Since f (x)gx f ( x) g x is constant with respect to f f, the derivative of f (x)gx f ( x) g x with respect to f f is 0 0 0 0An exact formula of the form f(xh)−f(x)hf0(x) =−f00(ξ), 2ξ∈(x, xh) (53)The slope of a linear function is calculated by rearranging the equation to its general form, f(x) = mx c;



Solved If F X 4x 2 3x 2 Evaluate F 1 State The Domain Of The Function F X X 3 X 1 Write The Equation Of The Line That Passes Th Course Hero




Numerical Differentiation Forward Difference Formula Ppt Download
Let's begin with f(xh)−f(x) Withf(x)=sin(x)f(xh)becomessin(xh) We need the trig identity for the sine of a sum of two angles sin(AB)=sinAcosBsinosA This means that f(xh)=sin(xh)=sin(x)cos(h)sin(h)cos(x) Still on the top, there is f(x), and it has a minus sign in front of it −f(x)becomes−sin(x) Now the top becomes the followingWrite the function in the form f(x)=a(xh)^{2}k by completing the square Then identify the vertex q(x)=2 x^{2}12 x11 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨Here, as x approaches 2, the limit of the function f(x) will be 5ie f(x) approaches 5 The value of the function which is limited and can be different than the limit value of the function itself Also, we can see that a function value may or may not be the same as




Question Video Using The Product Rule Nagwa



Calculus Index Cards
Find f (–1)" (pronounced as "fofx equals 2x plus three;I hope now you see that f(x h) = 1/(x h) 2 Thus for b, Write the two fractions with a common denominator and then simplify the numerator Write back and tell me what you got, Harley Math Central is supported by the University of Regina and TheMay 30, 18 · The derivative of \(f\left( x \right)\) with respect to x is the function \(f'\left( x \right)\) and is defined as, \\begin{equation}f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x h} \right) f\left( x \right)}}{h} \label{eqeq2}\end{equation}\



Derivative Of A Function




What Is Derivative Formula
Now, if you replace x with xh in any equation, its graph gets shifted to the right by a distance of h Similarly, Consider the graph of the parabola y = a x 2 Its vertex is clearly at (0, 0) Now, if you replace x with xDefined, respectively, in terms of the functional values f(x− h) and f(x), and f(x− h) and f(xh) Twopoint Forward Difference Formula (FDF) f′(x) ≈ f(xh) −f(x) h (73) Twopoint Backward Difference Formula (BDF) f′(x) ≈ f(x) −f(x−h) h (74) Twopoint Central Difference Formula (CDF) f′(x) ≈ f(xh) −f(x) h (75Problems involving derivatives 1) f(x) = 10x 4y, What is the first derivative f'(x) = ?




Best Act Math Formula Cheat Sheet Kiwi College Prep
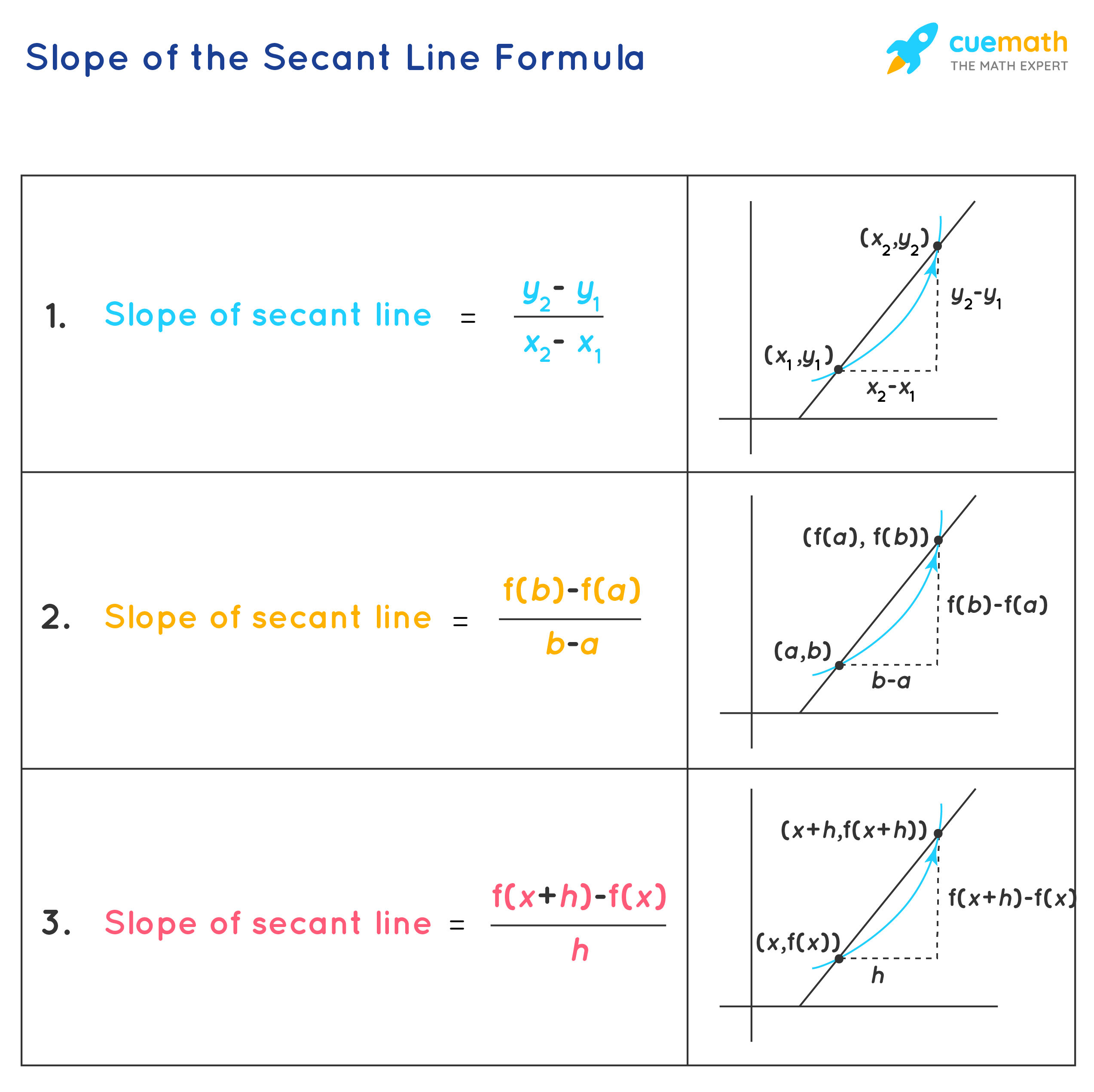



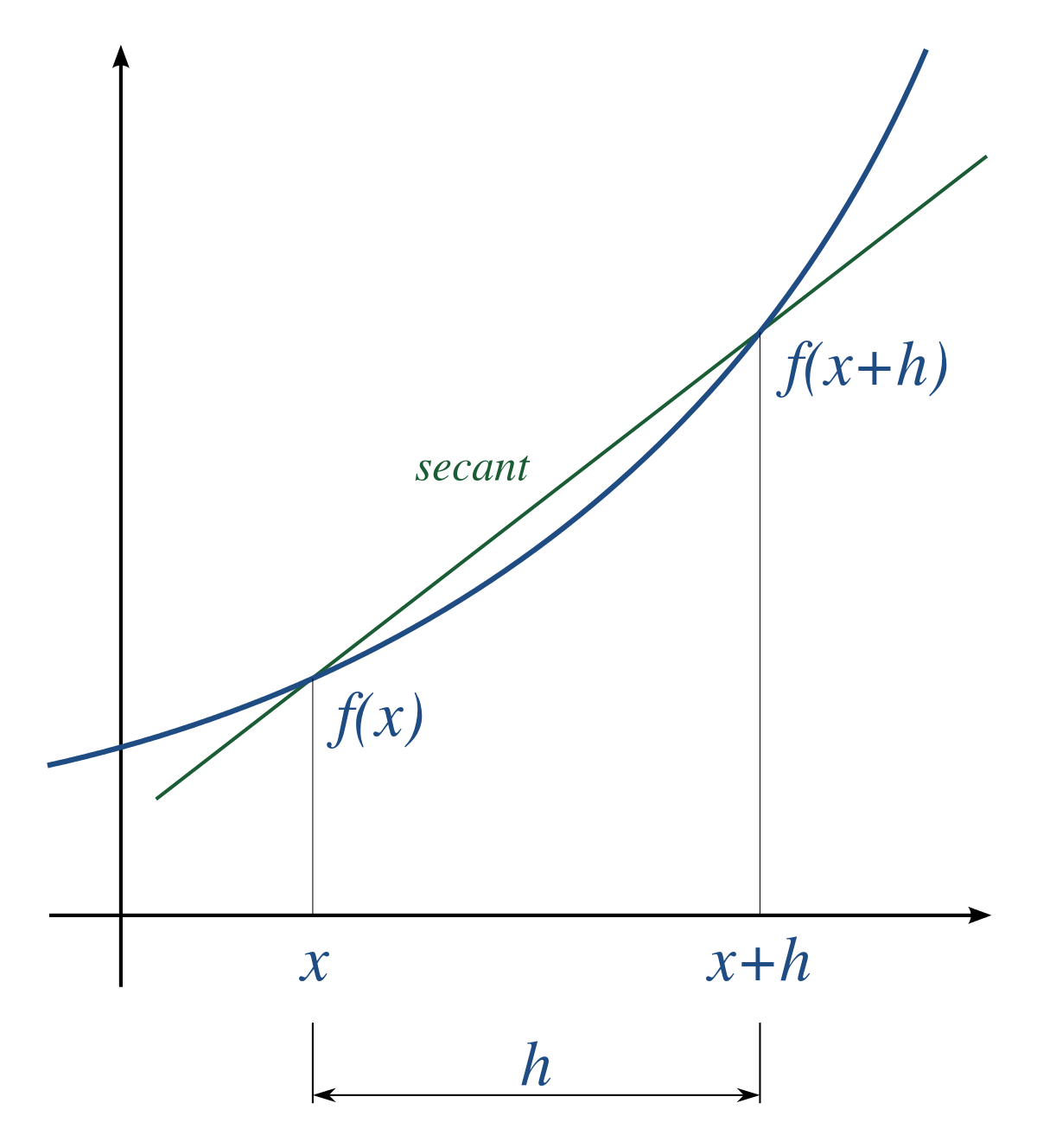
Slope Of The Secant Line Formula Learn The Formula To Find The Slope Of Secant Line
/////ABRIR/////No olviden darle like al video, suscriberse yH (f(x0 h)−f(x0))− h 2 f00(x0)− h2 6 f000(x0)O(h3) (3) Use extrapolation to derive an O(h3) formula for f0(x0) Solution In general, Richardson's extrapolation is used to generate highaccuracy approximations while using loworder formulas Replacing h in (3) with 2h gives the new formula f0(x0)= 1 2h (f(x0 2h)− f(x0))−hf00F x h f x f ′ x 1!




Ex 13 2 8 Find Derivative Of An X A For Constant A



Solved If F X 4x 2 3x 2 Evaluate F 1 State The Domain Of The Function F X X 3 X 1 Write The Equation Of The Line That Passes Th Course Hero
Concavity (new) End Behavior (new) Average Rate of Change (new) Holes (new) Piecewise Functions Continuity (new) Discontinuity (new) Arithmetic & Composition CompositionsFormula Difference quotient = (f(xh)f(x))/h Related Calculator Difference Quotient Calculator;The expression f (xh)f (x) over h, is called the difference quotient Determine the difference quotient of f (x)=2x^24x




If F X G X And H X Are Three Polynomials Of Degree 2 And Delta




Taylor Series In Numerical Differentiation Mathematics Stack Exchange
F(xh)−f(x) h = f(x)−f(x−∆x) ∆x is called the firstorder or O(∆x) backward difference approximation of f0(x) By combining different Taylor series expansions, we can obtain approximations of f0(x) of various orders For instance, subtracting the two expansions f(x∆x) = f(x)∆xf0(x)∆x2 f00(x) 2!Dec 01, · f' (x) = lim (f (xh) f (x))/h With the limit being the limit for h goes to 0 Finding the derivative of a function is called differentiation Basically, what you do is calculate the slope of the line that goes through f at the points x and xh Because we take the limit for h to 0, these points will lie infinitesimally close together;H2 where c is in x, x h;




Marthamatics 12
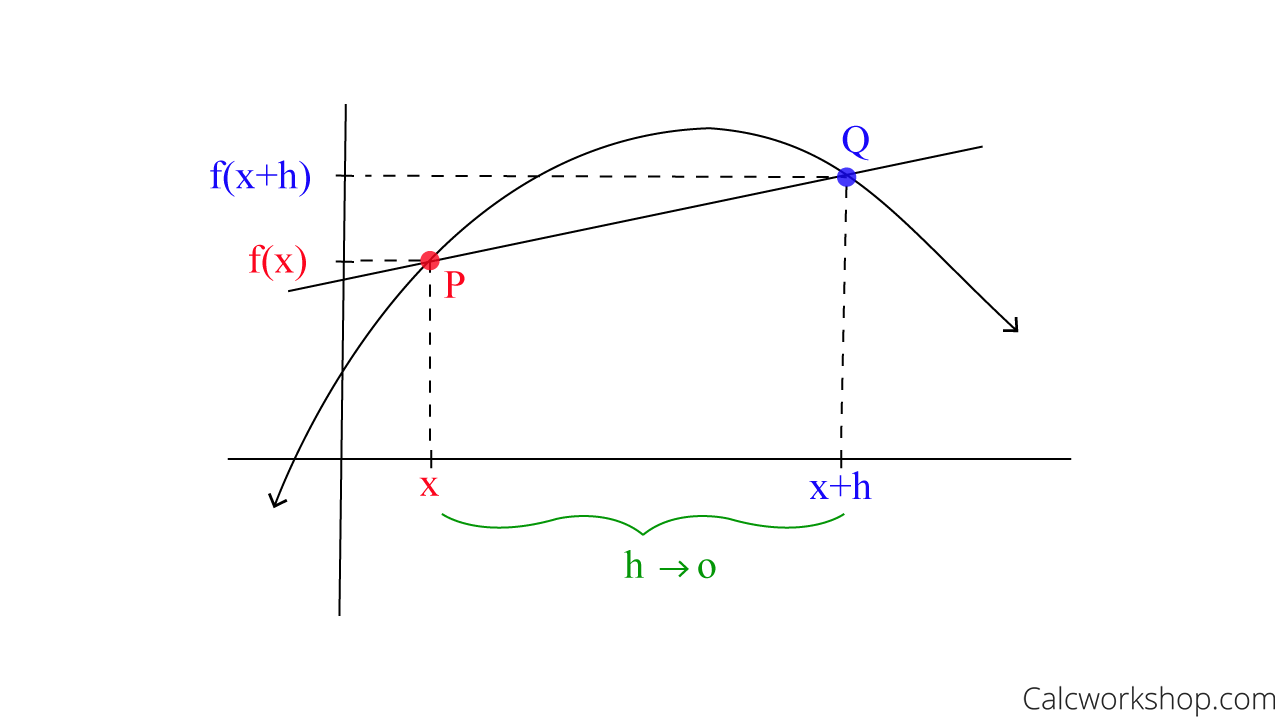



Definition Of Derivative Defined Illustrated W Examples
Derivation of the Quadratic Formula From this point, it is possible to complete the square using the relationship that x 2 bx c = (x h) 2 k Continuing the derivation using this relationship Recall that the ± exists as a function of computing a square root, making both positive and negative roots solutions of the quadratic equationF x −h f x − f ′ x 1!Nov 01, 17 · The normal Taylor expansion tells us that So how do you come from the original expansion to the second one?




Basics Of Derivatives
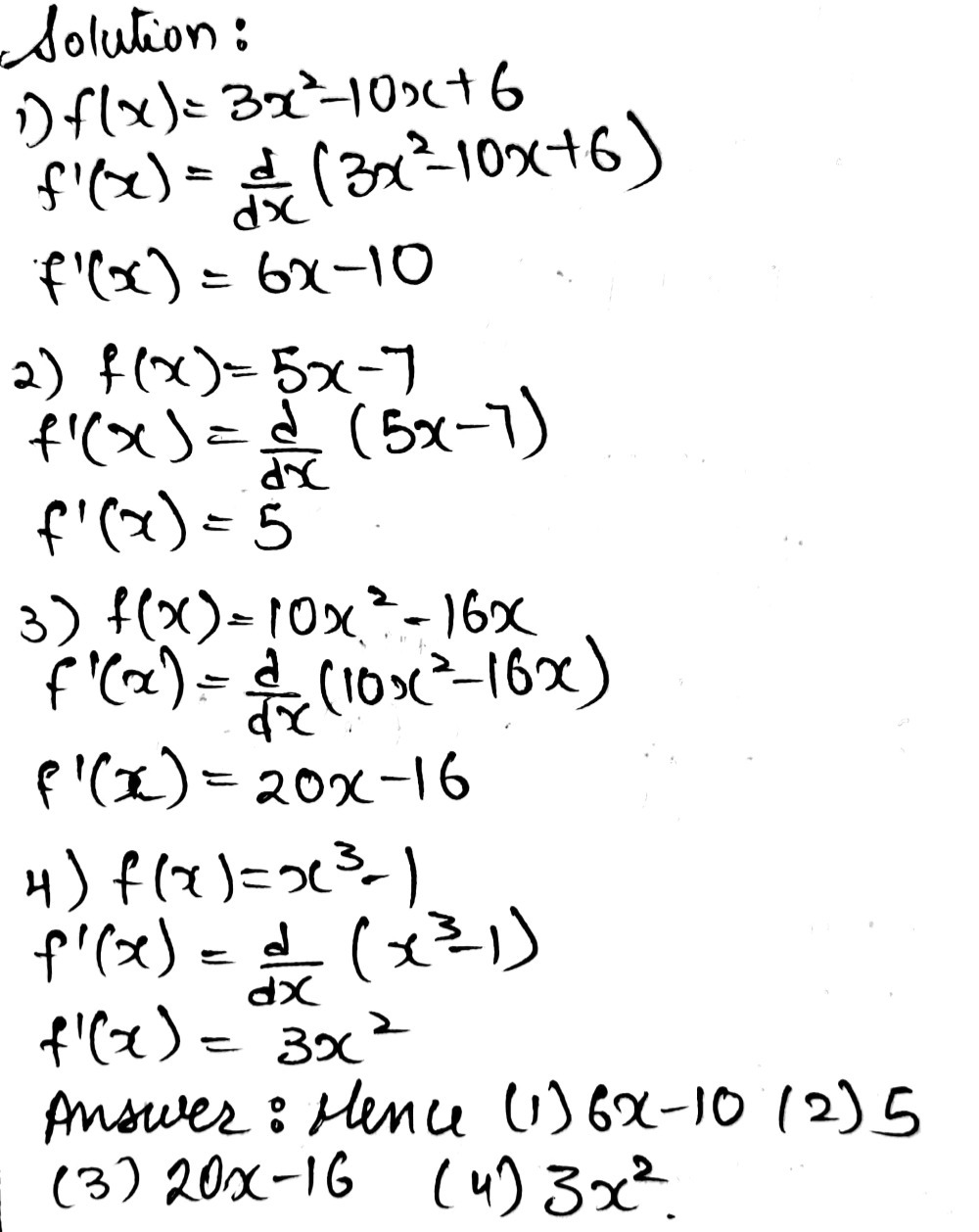



Ii Directions Find The Derivative Of The Followi Gauthmath
9 4 h a h 2 3 4 hb2 1 4 b −a 3a2 6ah 3h2 b2 1 4 b −a 3a2 2a b −a b −a 2 3 b2 1 4 b −a 3a2 2ab −2a2 b 2 −2ab a2 3 b2 1 4 b −a 4 3 a2 4 3 ab 4 3 b2 1 3 b −a a2 ab b2 1 3 b3 −a3 Example Suppose that the quadrature formula 0 2 f x dx c0f 0 c1f 1 c2f 2Dec 16, 14 · It's f^prime(g(h(x))) g^prime (h(x)) h^prime(x) Start by defining the function a(x)=g(h(x)) The the chain rule gives us (f @ g @ h)^prime (x)=(f @ alpha)^prime (x)=f^prime(alpha(x)) alpha^prime(x) Applying the definition of alpha(x) to the equation above gives us f^prime(alpha(x)) alpha^prime(x) = f^prime (g(h(x))) (g @h)^prime (x) Using the chain rule again f^prime (g(h(x))) (g @h∆x3 f000(ξ 1) 3!, ξ 1
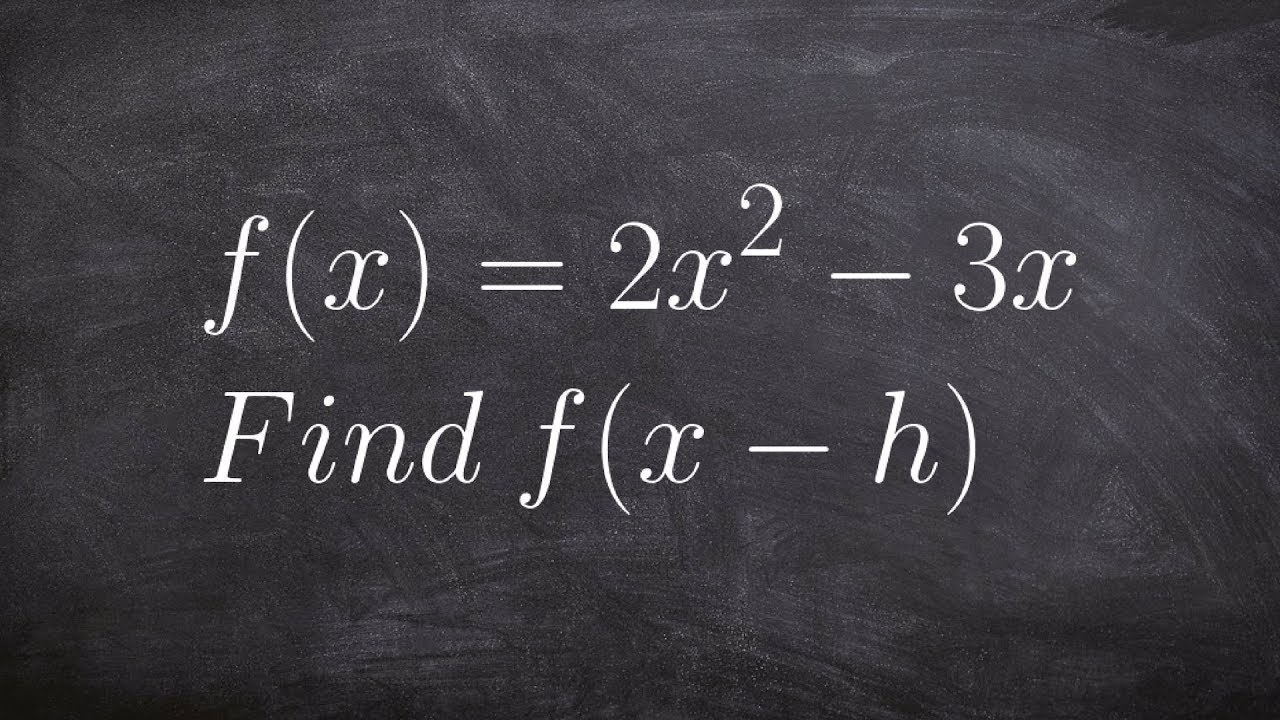



Evaluating A Function For An Algebraic Binomial Youtube




The Quotient Rule For Differentiation Math Insight
Oct 25, 09 · I am in a 12th grade Physics class and in the beginning of the year, we learned the calculus based equation f(xh) f(x)/h I understand that I am trying to simplify/solve for the answer when H goes to 0 (h > 0), and I understand that I must substitute f(x) into the given fields f(x) and f(xh)H f ′′ c 2!The graph of \(y = f (x h)~ ~\) is shifted \(h\) units to the right Note 244 At first, the direction of a horizontal translation may seem counterintuitive




Domain And Range Of Quadratic Functions Video Khan Academy




Numerical Analysis Approximation Error Problem Chegg Com
Let \(h\gt 0\text{}\) Compared with the graph of \(y = f (x)\text{,}\) the graph of \(y = f (x h)~ ~\) is shifted \(h\) units to the left, and;Oct 17, · $\dfrac{\Delta y}{\Delta x} = \dfrac{f(ah) – f(a)}{h}$ How to evaluate difference quotient?Why is (h,k) in the vertex formula of a parabola =a(xh)^2 k the vertex?
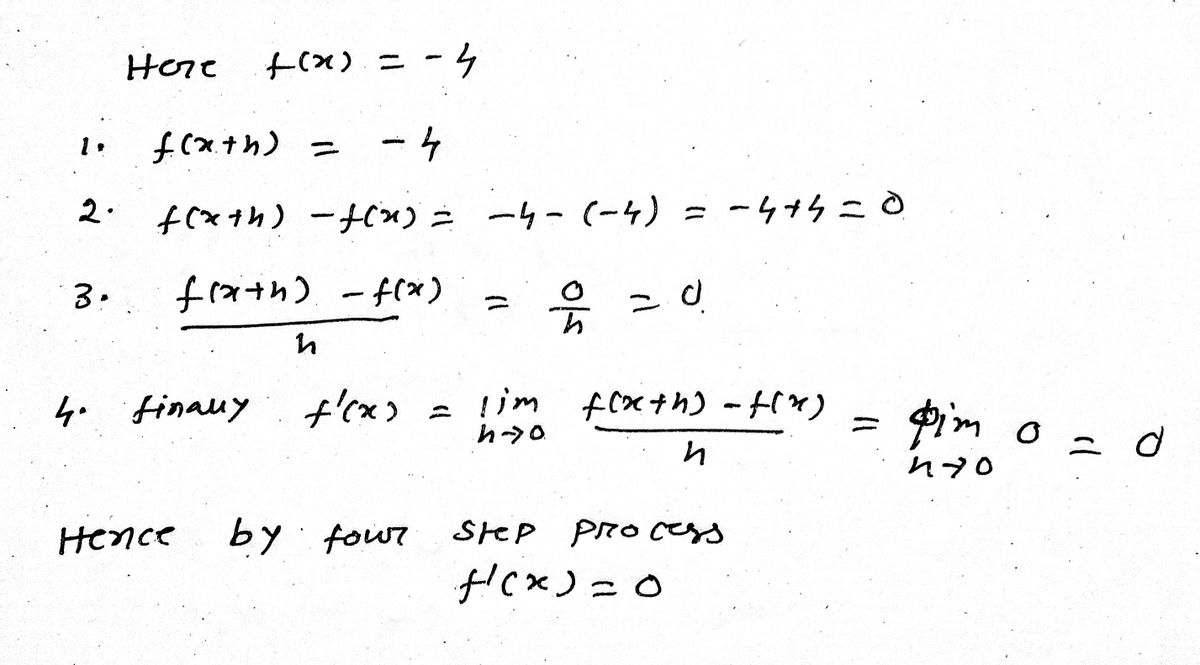



Answered Use The Four Step Process To Find F X Bartleby




Solutions Manual For Calculus For Business Economics Life Sciences And Social Sciences 13th Edition By Sullivan8 Issuu
Evaluate the Difference Quotient (f (xh)f (x))/h , f (x)=3/ (x^2) Consider the difference quotient formula Find the components of the definition Tap for more steps Evaluate the function at x = x h x = x h Tap for more steps Replace the variable x x with x h x h in the expressionH2 where c is in x −h, x Then f ′ x f x h −f x h − fH f ′′ c 2!




The Formula F X F X H F X H 2h Can Be Chegg Com
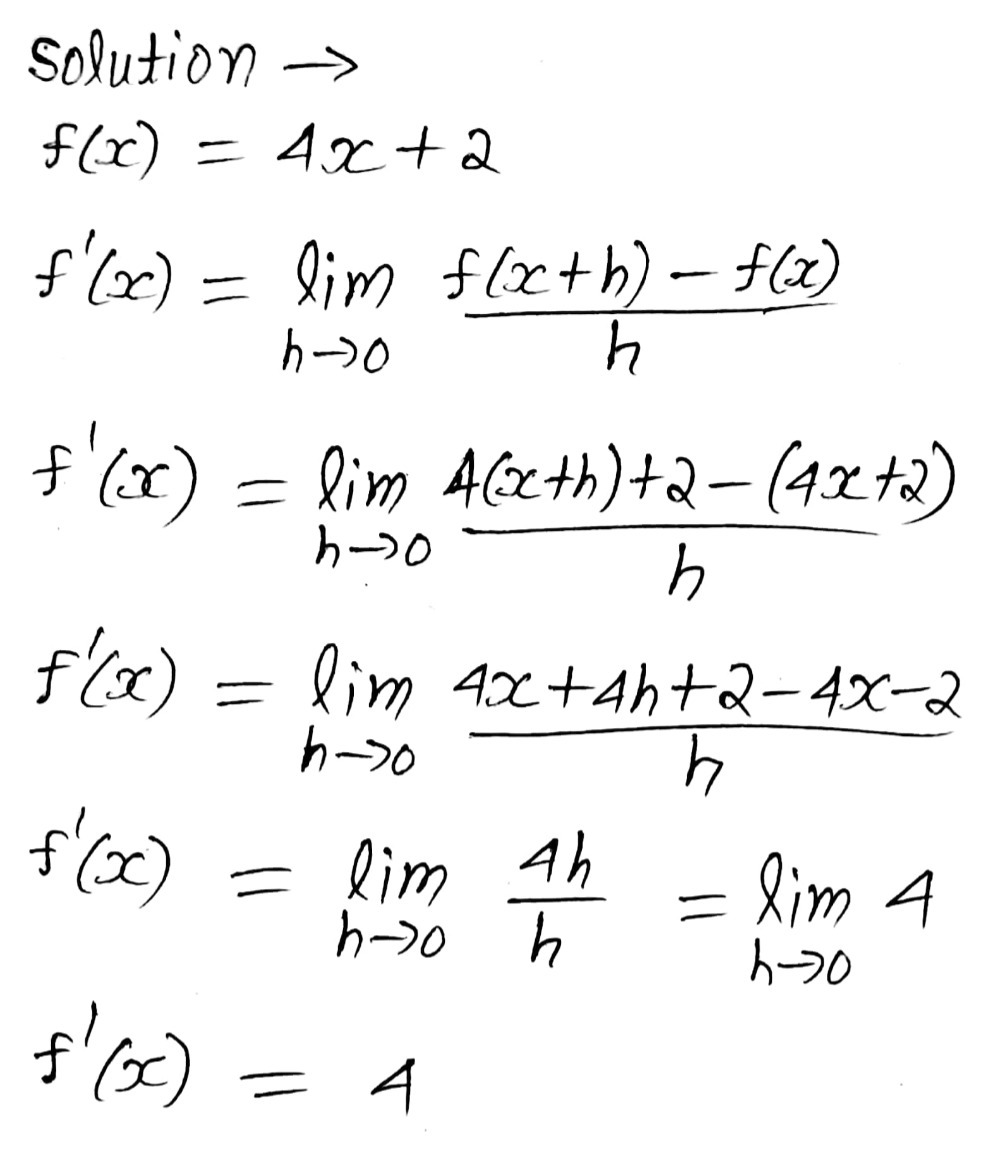



B Deterrmine The Derivatives Of The Functions U Gauthmath
Now you say "f (x) = 2x 3;\f'(x)=\lim_{h\rightarrow 0}\frac{f(xh)f(x)}{h} \ Finding an algebraic formula for the derivative of a function by using the definition above, is sometimes called differentiating from first principle By using a computer you can find numerical approximations of the derivative at all points of the graphUse the graph of the quadratic function f to write its formula as f (x)= a (x h)2 k f (x)= 6 a 4 G 8 14 112 2 24 62 Get more help from Chegg Solve it with




Pin On Differential Equations




Quadratic Function Wikipedia
A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesOct 04, 15 · Substitute ah and a for x in the formula for f(x) and simplify to find (f(ah)f(a))/h = 2a 2 h >f(x) = x^22x3 Then (f(ah) f(a))/h =(((ah)^22(ah)3) (a^22a3))/h =(color(red)(cancel(color(black)(a^2)))2ahh^2color(blue)(cancel(color(black)(2a)))2hcolor(green)(cancel(color(black)(3)))In mathematics, function composition is an operation that takes two functions f and g and produces a function h such that h(x) = g(f(x)) In this operation, the function g is applied to the result of applying the function f to x That is, the functions f X → Y and g Y → Z are composed to yield a function that maps x in X to g(f(x)) in Z
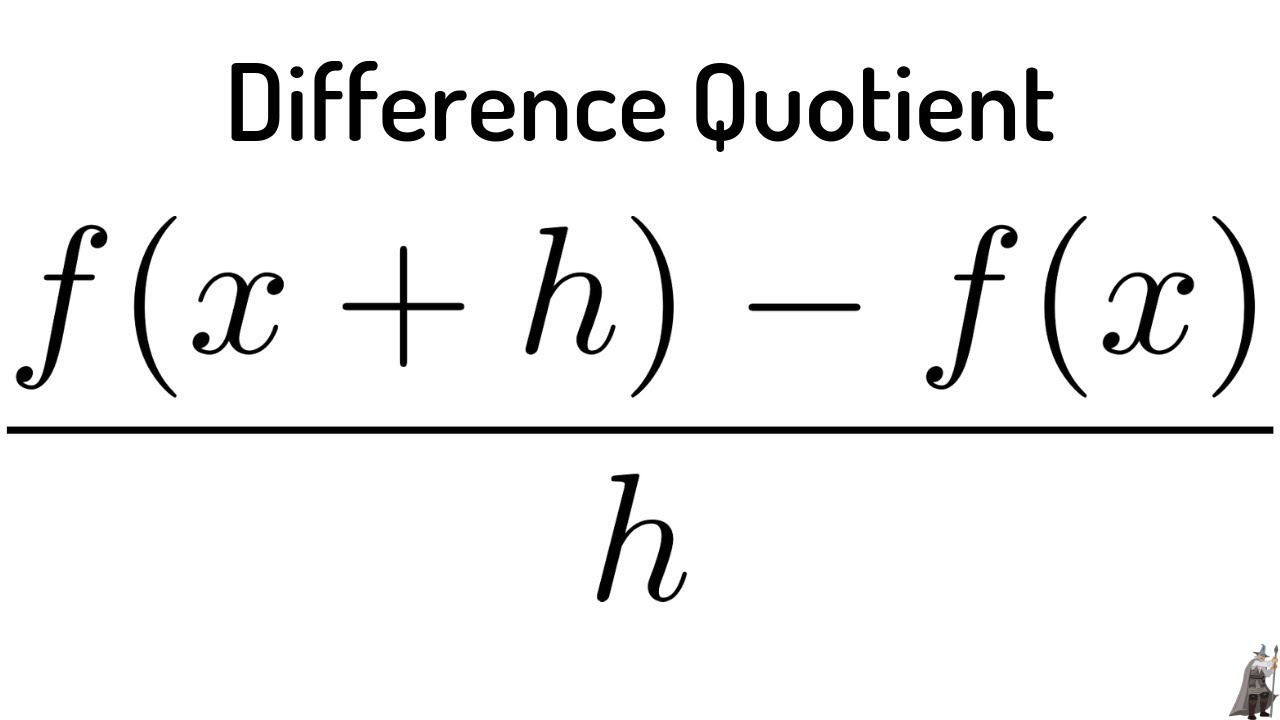



40 Find The Difference Quotient For F X 2x 2 5x Quadratic Example Youtube




The Derivative
Where (h, k) is the vertex$$ f(x h) = f(xh) f'(x h)(x(xh)) \frac{f''(xh)}{2!}(x(xh))^2 \frac{f'''(xh)}{3!} (x (x h))^3 \cdots $$ $$ = f(x h) hf'(xh) \frac{h^2}{2!}f''(x h)The x1 you might think shifts the graph to the left but it shifts it to the right So let's just review really quickly what this transformation does y equals half of x xh is a horizontal shift If each is positive it shifts the graph to the right Like when h was one, we had x1 the graph was shifted to the right one unit




Find The Difference Quotient F X H F X H Where H Does Not Equal Zero For The Function Below F X X 2 5 Simplify The Answer As Much As Possible Thank You Wyzant Ask An Expert
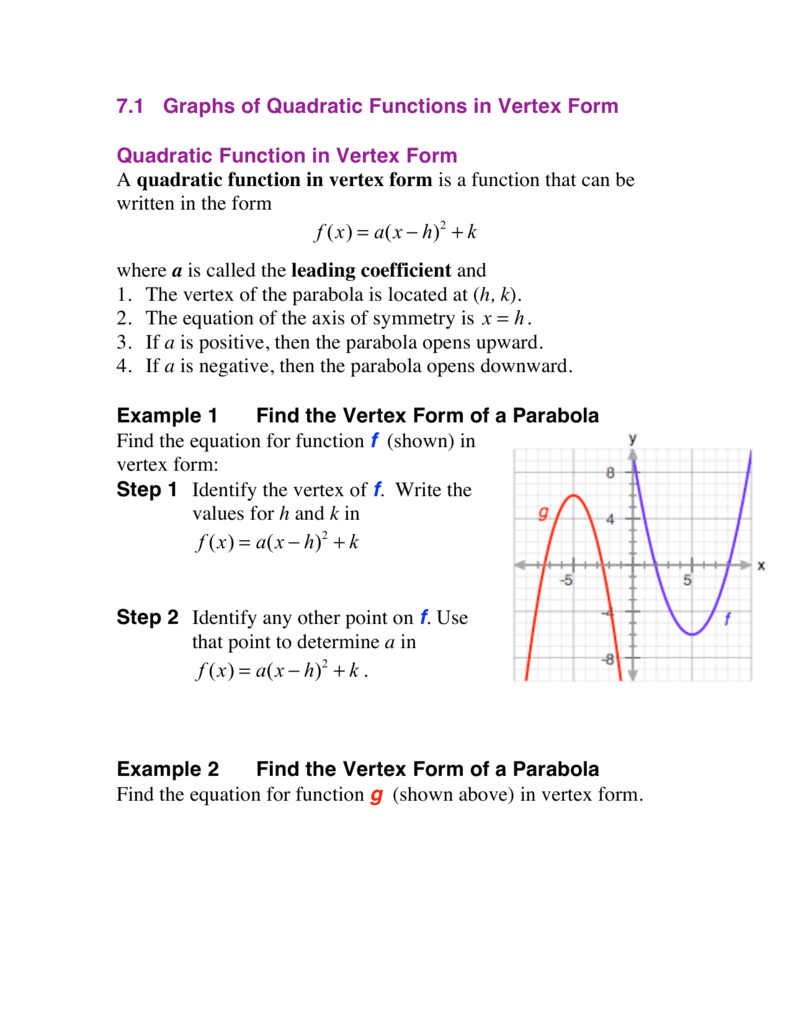



F X A X H 2 K F X A X H 2 K F X A X H 2 K
Find fofnegativeone") In either notation, you do exactly the same thing you plug –1 in for x , multiply by the 2 , and then add in the 3 , simplifying to get a final value of 1Generate the approximation formula f' (x) ~ 1 1 4f (xh) 3f (x)f ( 2h) 2h with the error termIn this chapter we investigate how the limit definition of the derivative leads to interesting patterns and rules that enable us to quickly find a formula for \(f'(x)\) without directly using the limit definition For example, we would like to apply shortcuts to differentiate a function such as \(g(x) = 4x^7 \sin(x) 3e^x\text{}\)
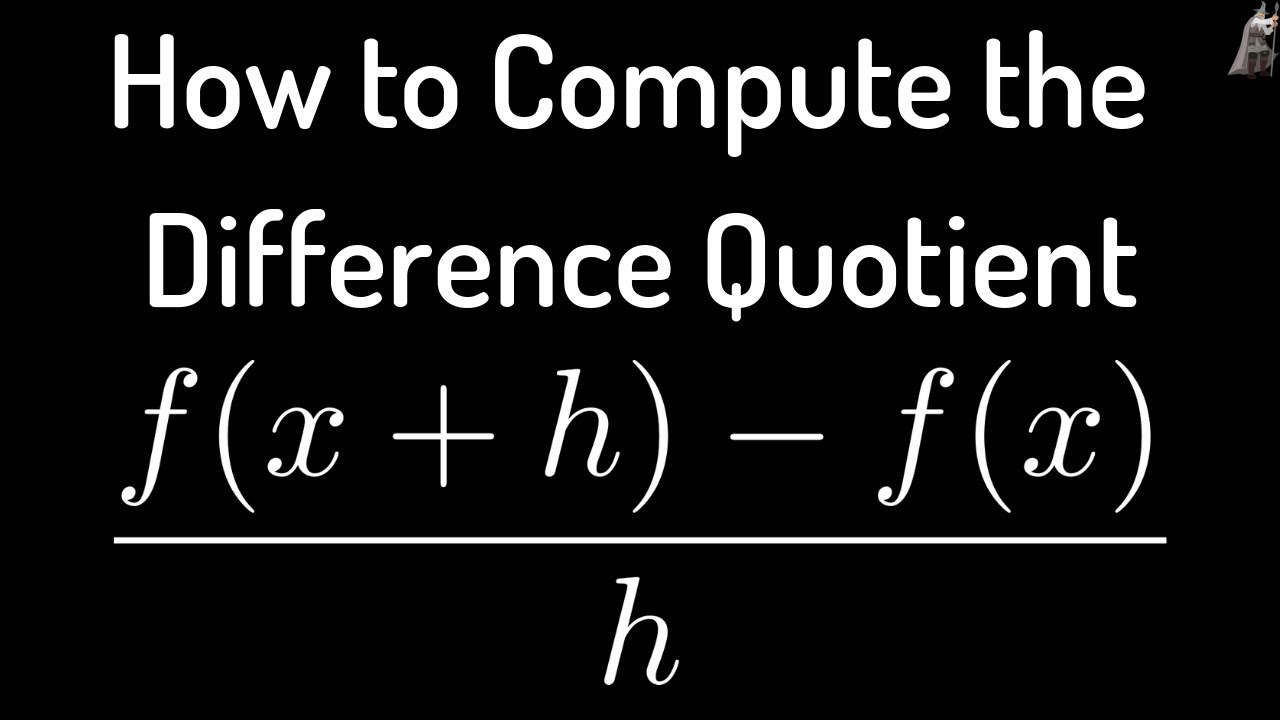



How To Compute The Difference Quotient F X H F X H Youtube




06 Numerical Differentiation Integration 1 Integral Derivative
And therefore, it is the slope of the function in the point x




If F X Sqrt X 2 1 G X X 1 X 2 1 And H X 2x 3 The




Quadratic Functions




5 Numerical Differentiation Pdf Free Download




Solved The Formula 3 Is The Centered Formula F X F X Chegg Com




The Derivative




How To Graph A Quadratic Equation 10 Steps With Pictures




Numerical Differentiation Forward Difference Formula Ppt Download
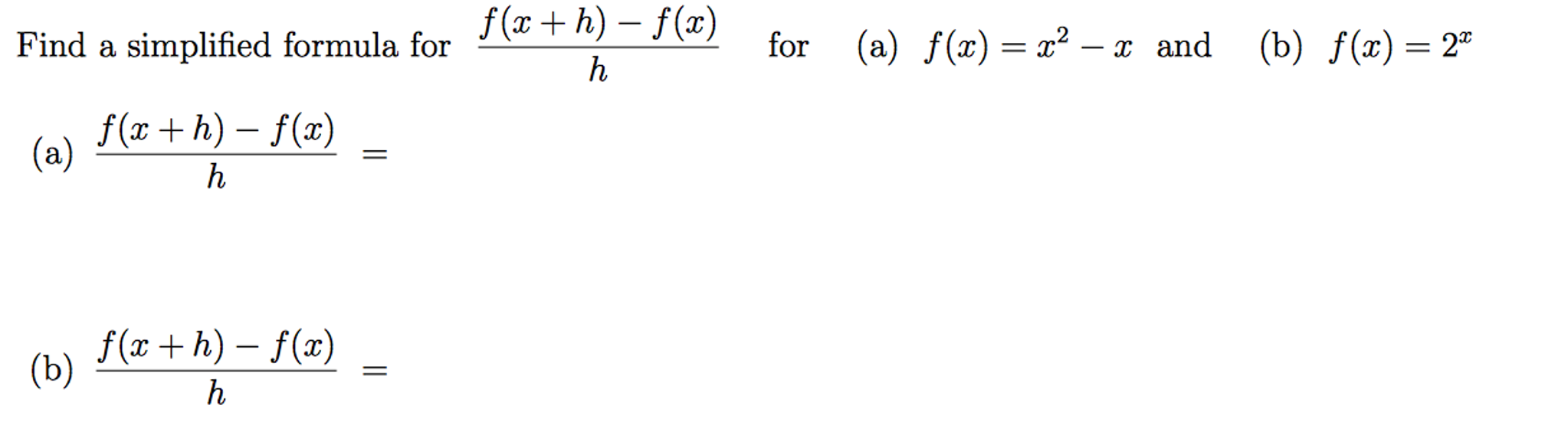



Find The Simplified Formula For F X H F X H For Chegg Com



Numerical Differentiation Wikipedia



Derivative Of A Function




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily




Quadratic Functions




Parabolas And The Distance Formula Read Calculus Ck 12 Foundation
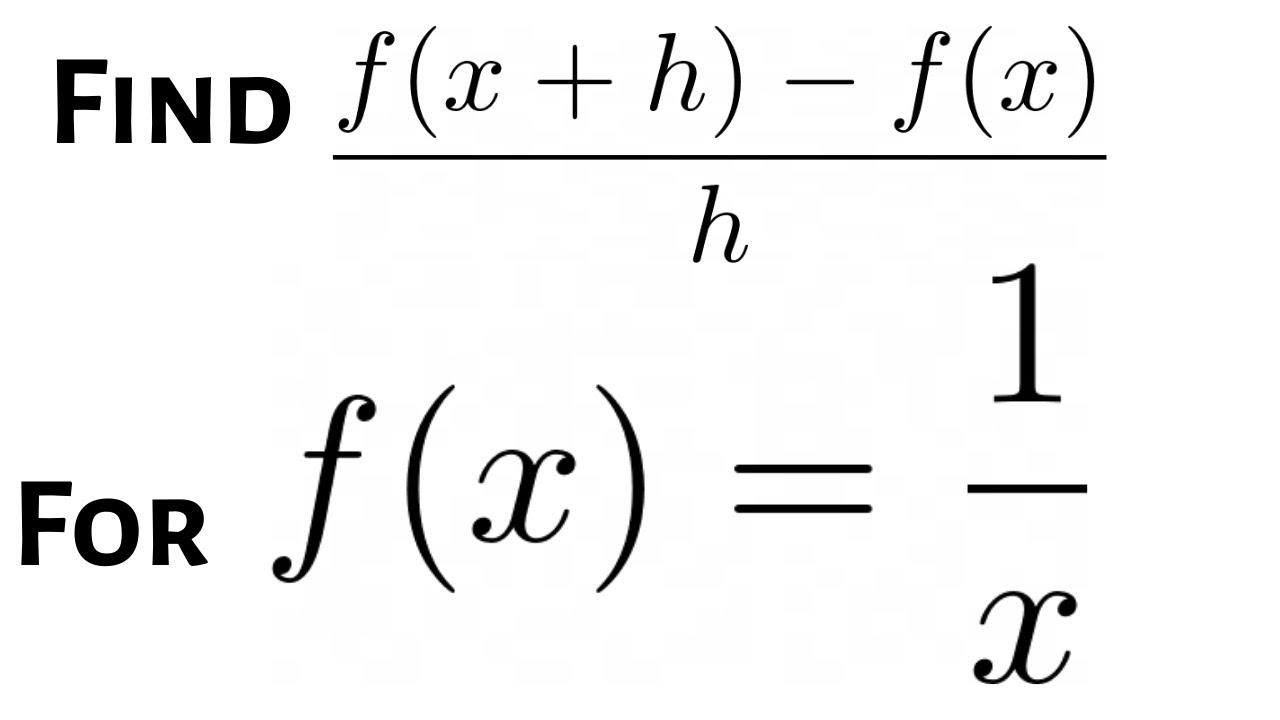



How To Find The Difference Quotient F X H F X H For F X 1 X Youtube




Even And Odd Functions Equations Video Khan Academy




Calculating A Derivative Using The Definition Of A Derivative Example 1 Youtube




Ppt Numerical Differentiation Powerpoint Presentation Free Download Id 5987




Numerical Differentiation Forward Difference Formula Ppt Download



Solved Use The Graph Of A Quadratic Function F To Write Its Formula As F X A X H 2 K F X Course Hero




Vertex Form Introduction Video Khan Academy




If F Is A Differentiable Function Of X Then Lim H 0 F X




Numerical Differentiation Forward Difference Formula Ppt Download




Basics Of Derivatives




Little Genius Female Child On Hand Drawings Math Science Formula Pattern Kids Mathematics Education Concept Stock Photo Alamy




Derivatives Of Inverse Functions From Equation Video Khan Academy
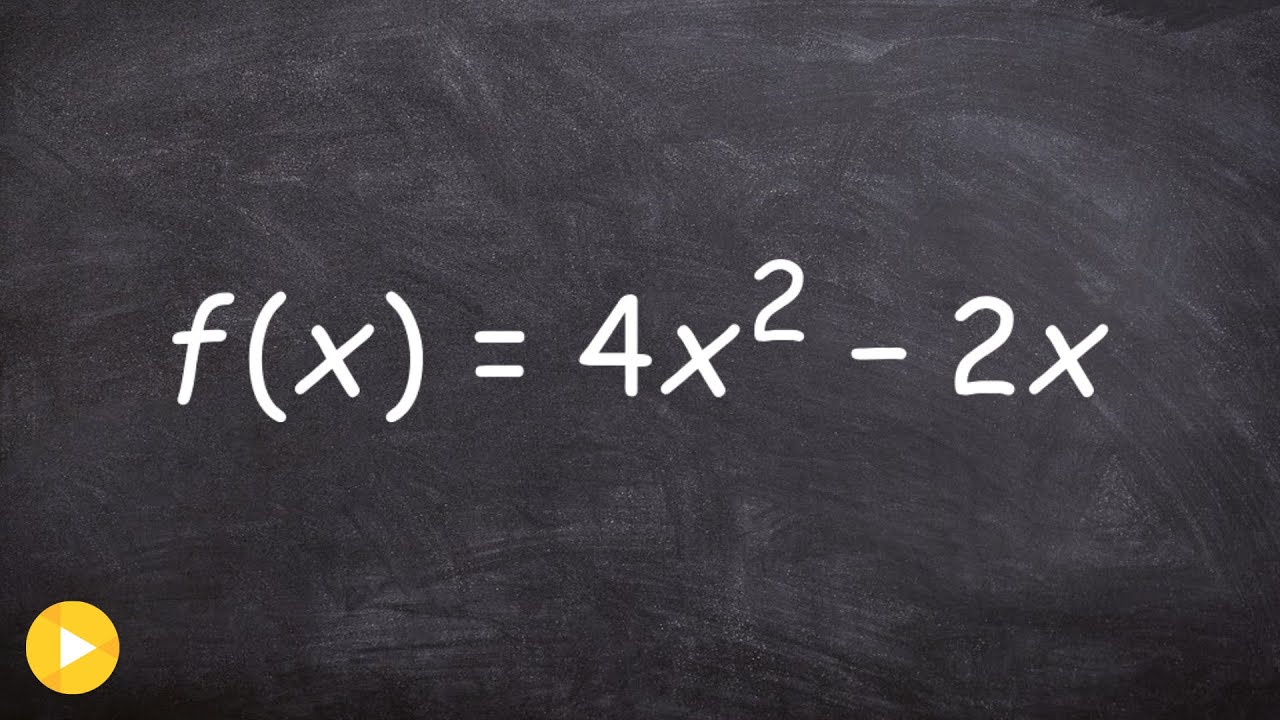



Simplifying The Difference Quotient Youtube
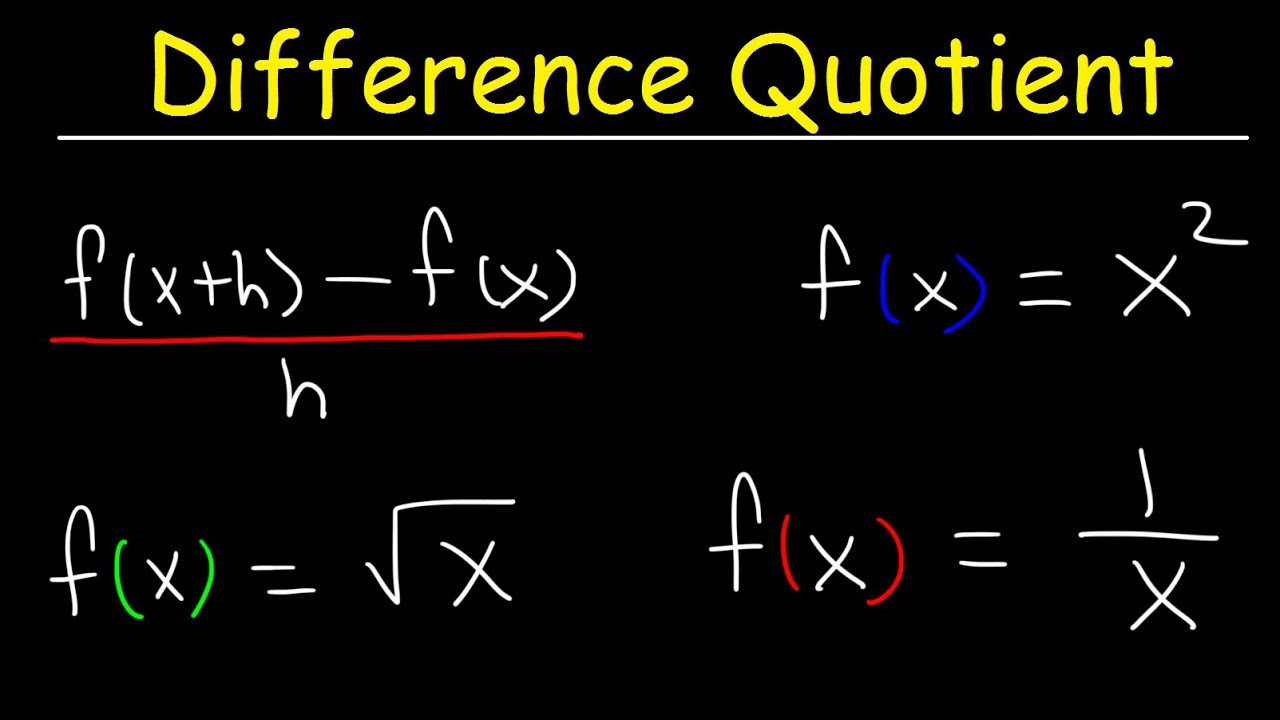



Difference Quotient Youtube




If F X G X G X 2 2 H X H X 1 Where G And H




Warm Up Find The Difference Quotient Ppt Download
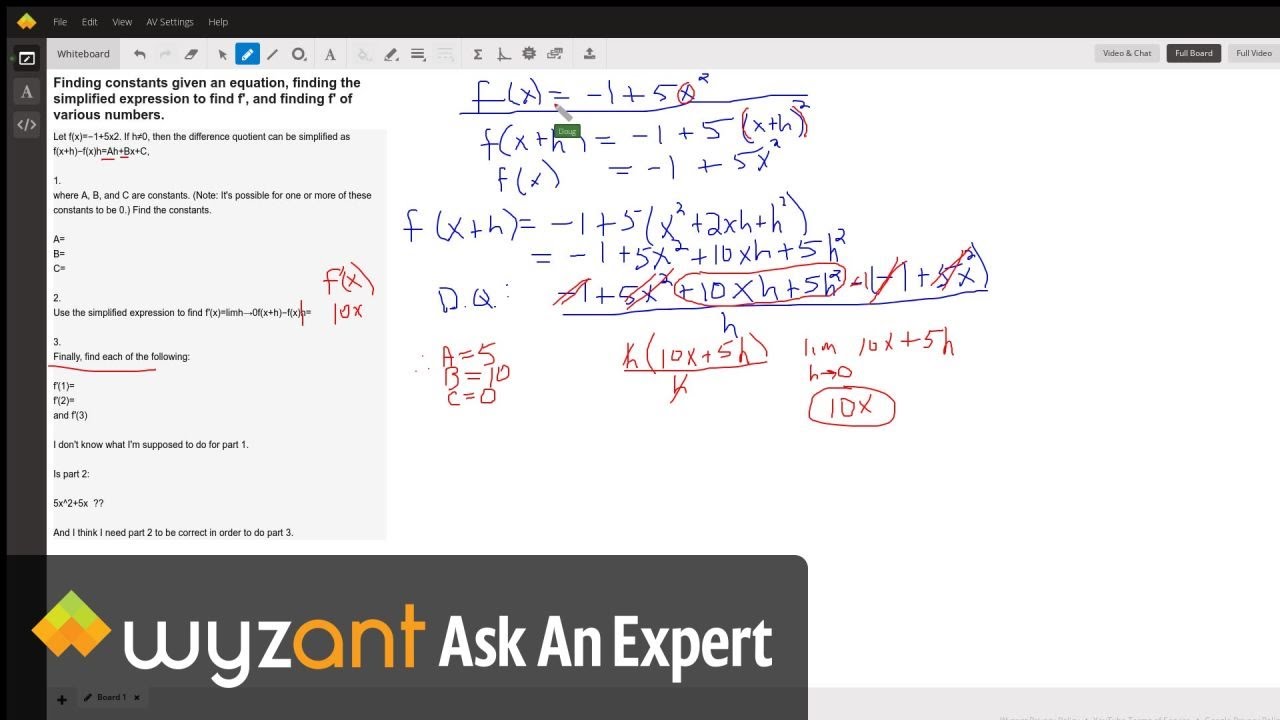



Finding Constants Given An Equation Finding The Simplified Expression To Find F And Finding F Of Various Numbers Wyzant Ask An Expert
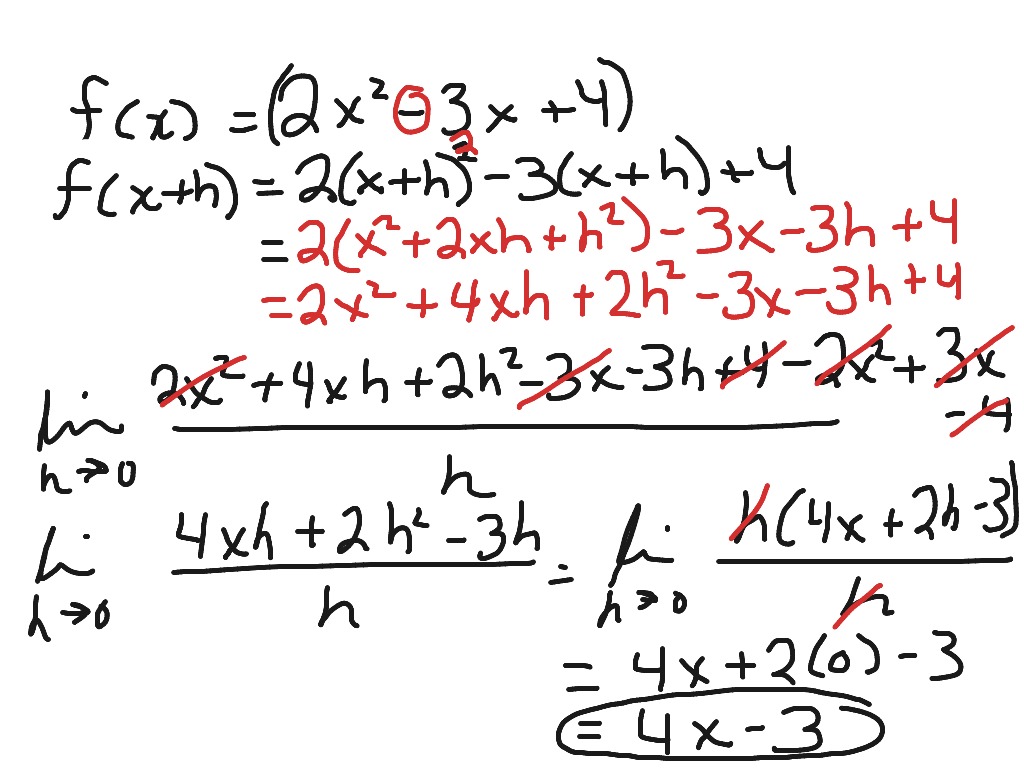



Derivative Of 2x 2 3x 4 Math Calculus Showme




F X H F X F X H F X 2h Consider The Approximation Chegg Com




3 In Class We Discussed The Central Difference Chegg Com
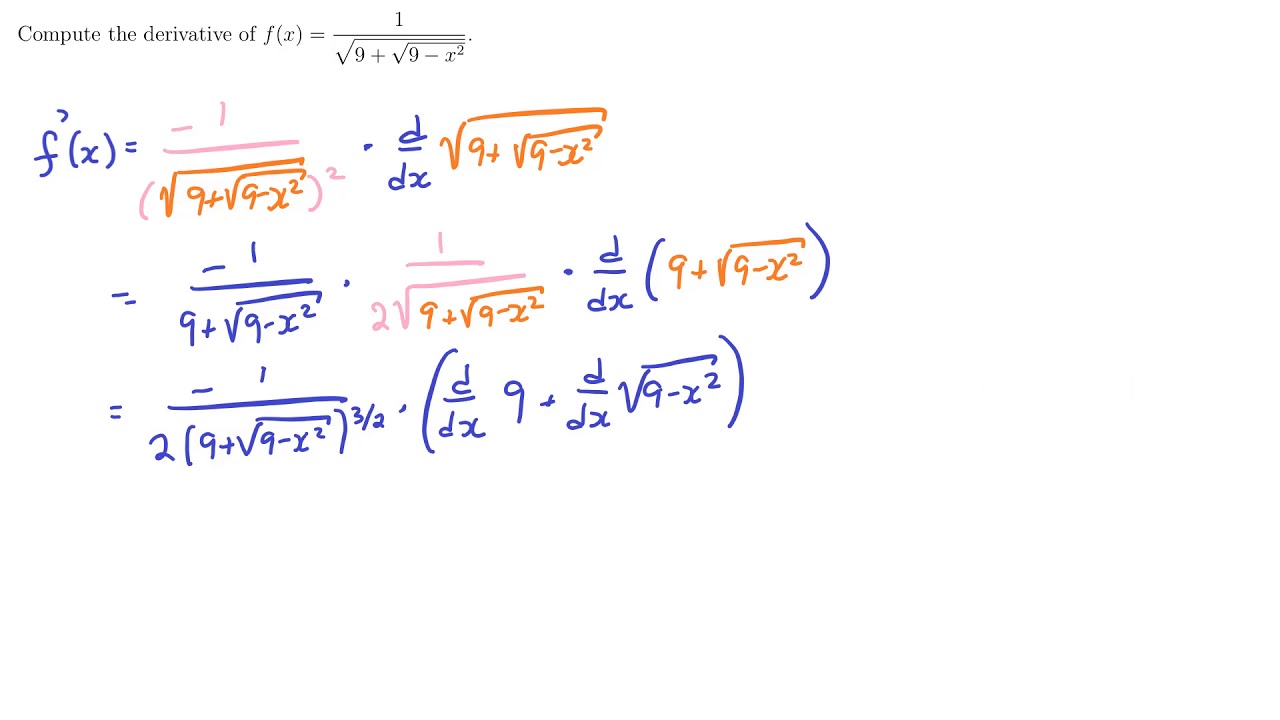



The Chain Rule




Difference Quotient Examples Videos Worksheets Solutions Activities




Solved F X H F X H Explain Why Should Give A Reasonabl Chegg Com




Numerical Differentiation Forward Difference Formula Ppt Download



Solved If F X 4x 2 3x 2 Evaluate F 1 State The Domain Of The Function F X X 3 X 1 Write The Equation Of The Line That Passes Th Course Hero




Finding The Equation Of A Transformation From The Graph Youtube



Calculus Index Cards




Finding Features Of Quadratic Functions Video Khan Academy




Ppt Numerical Differentiation Powerpoint Presentation Free Download Id 5987




Find The Derivative Of A Function At A Certain Num Gauthmath




Numerical Differentiation Ppt Download




Mathtype Usually When Deriving A Function More Than Once One Just Derives And Then Derives Again And So On Alternatively There Is This Nice Formula Involving Pascal S Triangle To Calculate




Numerical Differentiation Forward Difference Formula Ppt Download
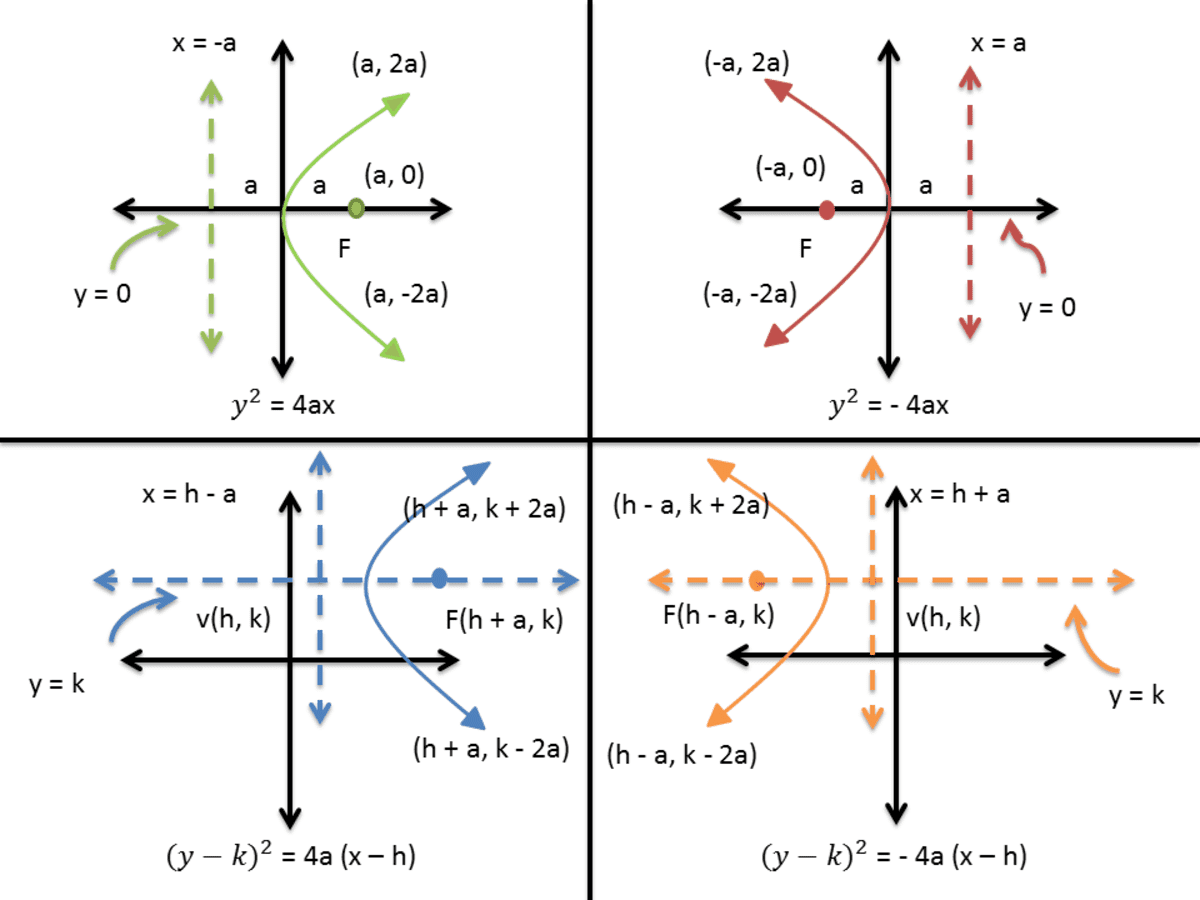



How To Graph A Parabola In A Cartesian Coordinate System Owlcation




Basics Of Derivatives




5 Numerical Differentiation Pdf Free Download




Example 16 Compute Derivative Of Sin X Chapter 13 Class 11


